激活函数
标签:激活函数, activation function目录
- 1. Step
- 2. Identity
- 3. ReLU
- 4. Sigmoid
- 5. Tanh
- 6. Leaky Relu
- 7. PReLU
- 8. RReLU
- 9. ELU
- 10. SELU
- 11. SReLU
- 12. Hard Sigmoid
- 13. Hard Tanh
- 14. LeCun Tanh
- 15. ArcTan
- 16. SoftSign
- 17. SoftPlus
- 18. Signum
- 19. Bent Identity
- 20. Symmetrical Sigmoid
- 21. Log Log
- 22. Gaussian
- 23. Absolute
- 24. Sinusoid
- 25. Cos
- 26. Sinc
参考26种神经网络激活函数可视化,原文Visualising Activation Functions in Neural Networks【可以在里面选择不同的激活函数,看图】
1. Step
激活函数 Step 更倾向于理论而不是实际,它模仿了生物神经元要么全有要么全无的属性。它无法应用于神经网络,因为其导数是 0(除了零点导数无定义以外),这意味着基于梯度的优化方法并不可行。
\[
f(x) =\begin{cases}1 & \text{for } x\geq0\\0 & \text{for } x<0\end{cases}
\]
\[
f'(x) =\begin{cases}0 & \text{for } x\neq0\\? & \text{for } x=0\end{cases}
\]
2. Identity
通过激活函数 Identity,节点的输入等于输出。它完美适合于潜在行为是线性(与线性回归相似)的任务。当存在非线性,单独使用该激活函数是不够的,但它依然可以在最终输出节点上作为激活函数用于回归任务。
\[
\begin{align*}f(x) = x\end{align*}
\]
\[
\begin{align*}f'(x) = 1\end{align*}
\]
3. ReLU
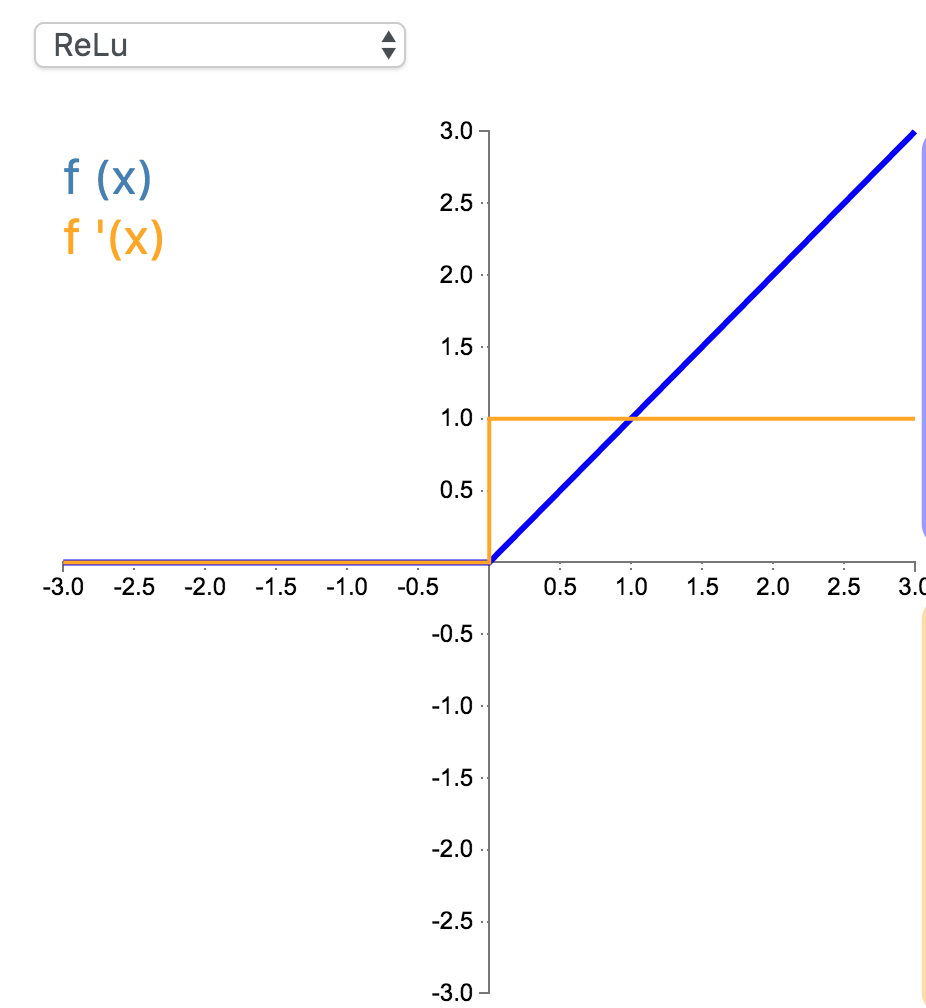
修正线性单元(Rectified linear unit,ReLU)是神经网络中最常用的激活函数。它保留了 step 函数的生物学启发(只有输入超出阈值时神经元才激活),不过当输入为正的时候,导数不为零,从而允许基于梯度的学习(尽管在 x=0 的时候,导数是未定义的)。使用这个函数能使计算变得很快,因为无论是函数还是其导数都不包含复杂的数学运算。然而,当输入为负值的时候,ReLU 的学习速度可能会变得很慢,甚至使神经元直接无效,因为此时输入小于零而梯度为零,从而其权重无法得到更新,在剩下的训练过程中会一直保持静默。
\[
f(x) =\begin{cases}x & \text{for } x\geq0\\0 & \text{for } x<0\end{cases}
\]
\[
f'(x) =\begin{cases}1 & \text{for } x\geq0\\0 & \text{for } x<0\end{cases}
\]
4. Sigmoid
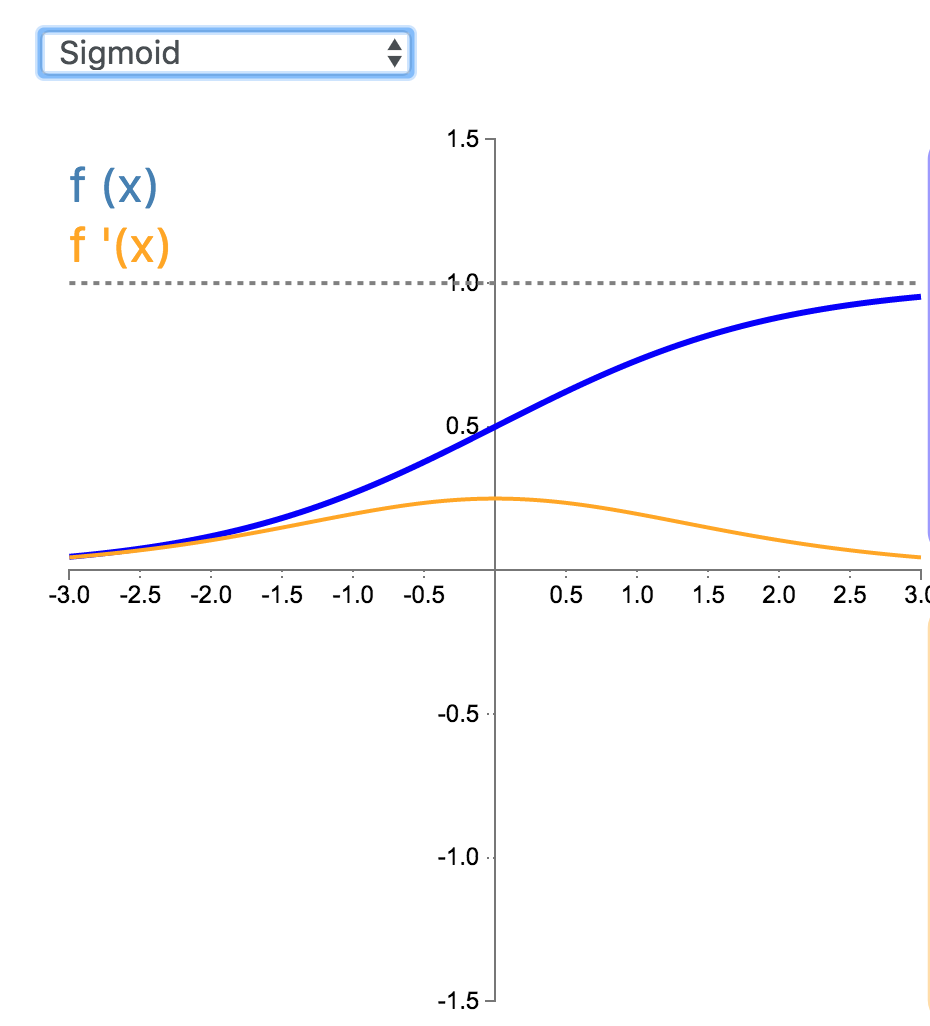
Sigmoid 因其在 logistic 回归中的重要地位而被人熟知,值域在 0 到 1 之间。Logistic Sigmoid(或者按通常的叫法,Sigmoid)激活函数给神经网络引进了概率的概念。它的导数是非零的,并且很容易计算(是其初始输出的函数)。然而,在分类任务中,sigmoid 正逐渐被 Tanh 函数取代作为标准的激活函数,因为后者为奇函数(关于原点对称)。
\[
\begin{align*}f(x) = \frac{1}{1 + e^{-x}} \end{align*}
\]
\[
\begin{align*}f'(x) &= \frac{e^{-x}}{(1+e^{-x})^2} \\&= f(x)(1-f(x)) \end{align*}
\]
5. Tanh
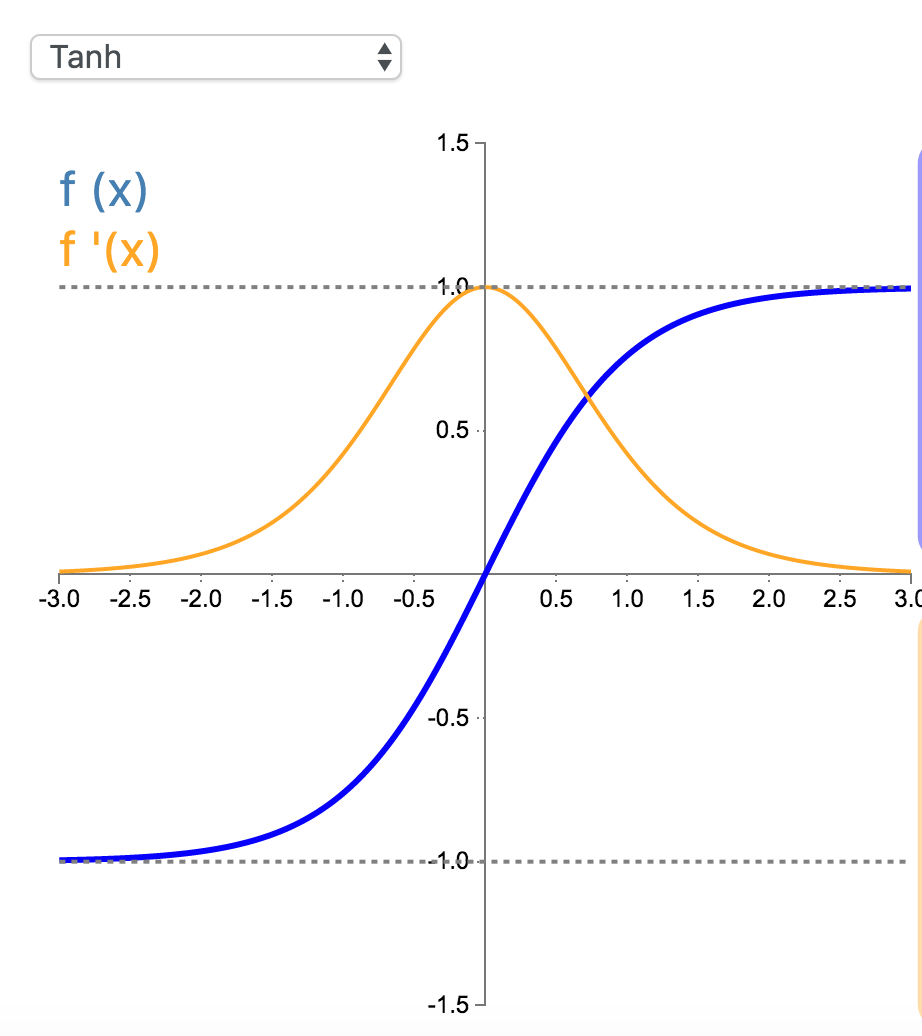
在分类任务中,双曲正切函数(Tanh)逐渐取代 Sigmoid 函数作为标准的激活函数,其具有很多神经网络所钟爱的特征。它是完全可微分的,反对称,对称中心在原点。为了解决学习缓慢和/或梯度消失问题,可以使用这个函数的更加平缓的变体(log-log、softsign、symmetrical sigmoid 等等)。
\[
\begin{align*}f(x)&=\tanh(x)\\&=\frac{2}{1+e^{-2x}}-1\end{align*}
\]
\[
\begin{align*}f'(x)&=1-\tanh^2(x)\\&=1-f(x)^2\end{align*}
\]
6. Leaky Relu
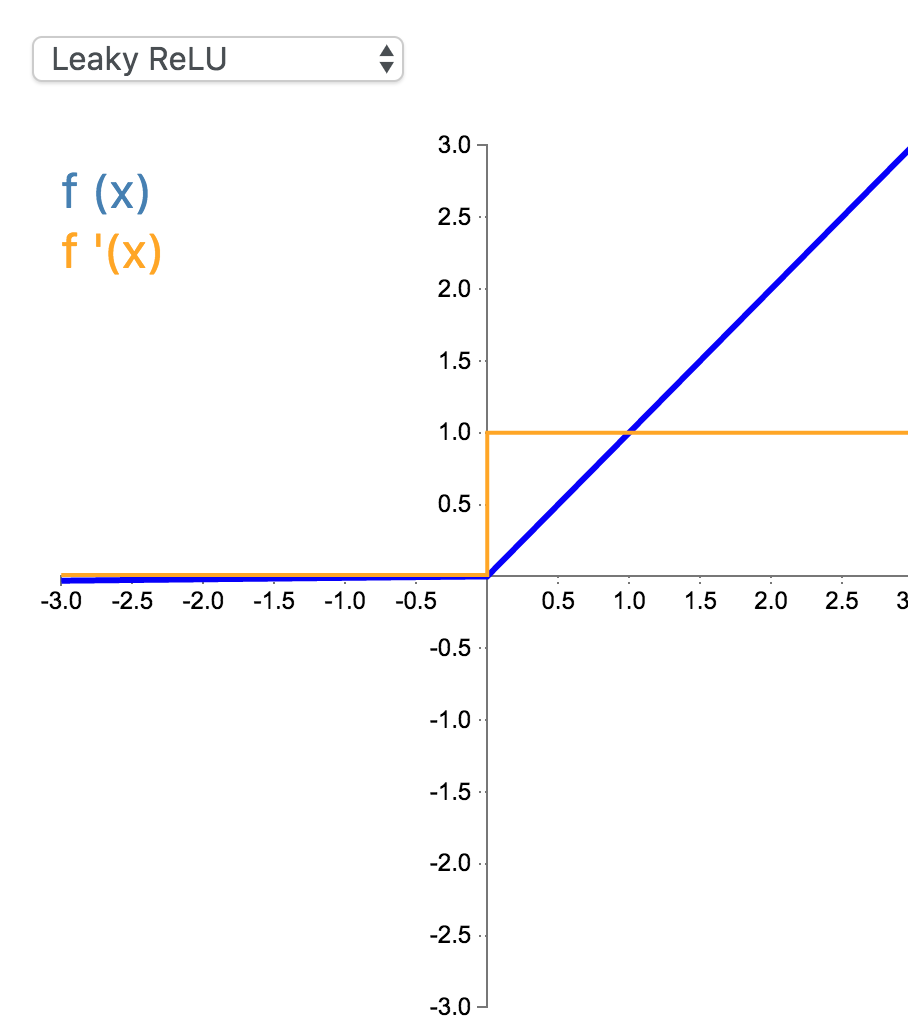
经典(以及广泛使用的)ReLU 激活函数的变体,带泄露修正线性单元(Leaky ReLU)的输出对负值输入有很小的坡度。由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习(虽然会很慢)。
\[
f(x) =\begin{cases}x & \text{for } x\geq0\\0.01x & \text{for } x<0\end{cases}
\]
\[
f'(x) =\begin{cases}1 & \text{for } x\geq0\\0.01 & \text{for } x<0\end{cases}
\]
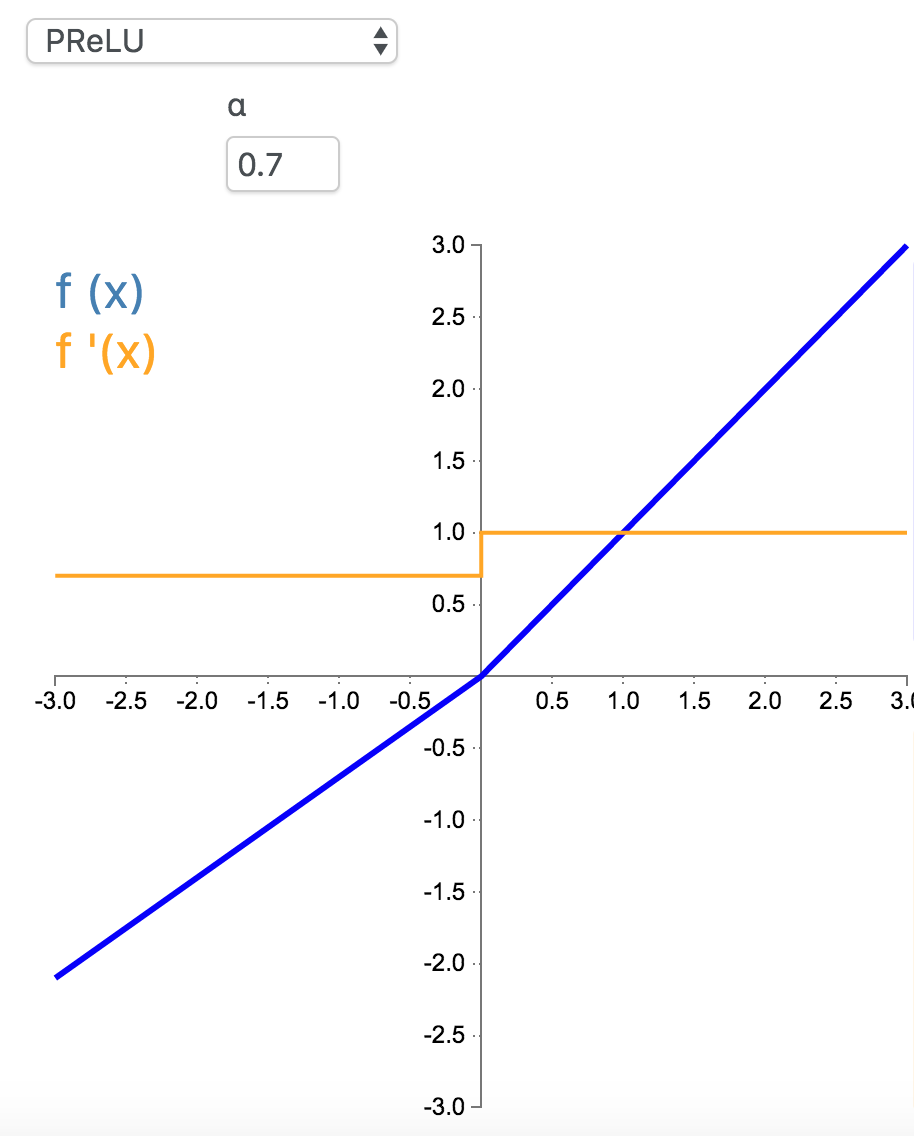
7. PReLU
参数化修正线性单元(Parameteric Rectified Linear Unit,PReLU)属于 ReLU 修正类激活函数的一员。它和 RReLU 以及 Leaky ReLU 有一些共同点,即为负值输入添加了一个线性项。而最关键的区别是,这个线性项的斜率实际上是在模型训练中学习到的。
\[
f_{\alpha}(x) =\begin{cases}x & \text{for } x\geq0\\\alpha x & \text{for } x<0\end{cases}\]
\[
f'_{\alpha}(x) =\begin{cases}1 & \text{for } x\geq0\\\alpha & \text{for } x<0\end{cases}
\]
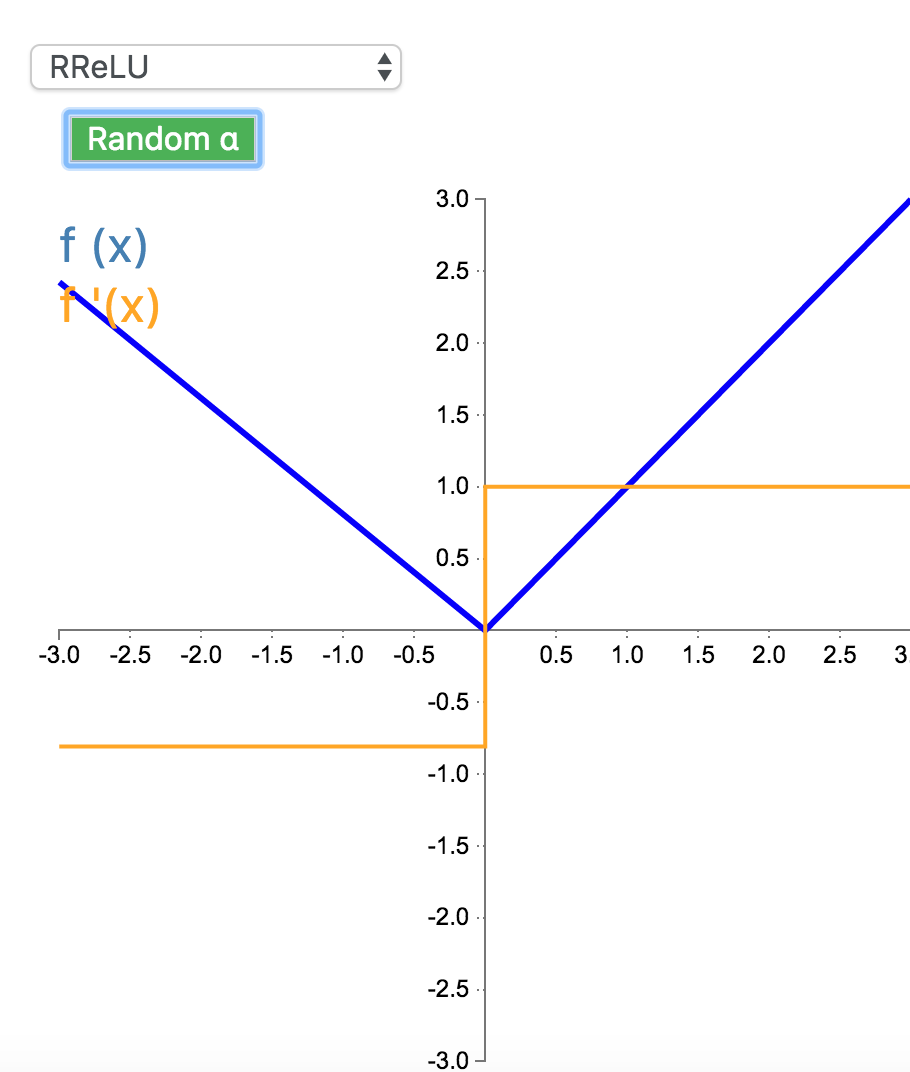
8. RReLU
随机带泄露的修正线性单元(Randomized Leaky Rectified Linear Unit,RReLU)也属于 ReLU 修正类激活函数的一员。和 Leaky ReLU 以及 PReLU 很相似,为负值输入添加了一个线性项。而最关键的区别是,这个线性项的斜率在每一个节点上都是随机分配的(通常服从均匀分布)。
\[
f(x) =\begin{cases}x & \text{for } x\geq0\\\alpha x & \text{for } x<0\end{cases}\]
\[
f'(x) =\begin{cases}1 & \text{for } x\geq0\\\alpha & \text{for } x<0\end{cases}
\]
9. ELU
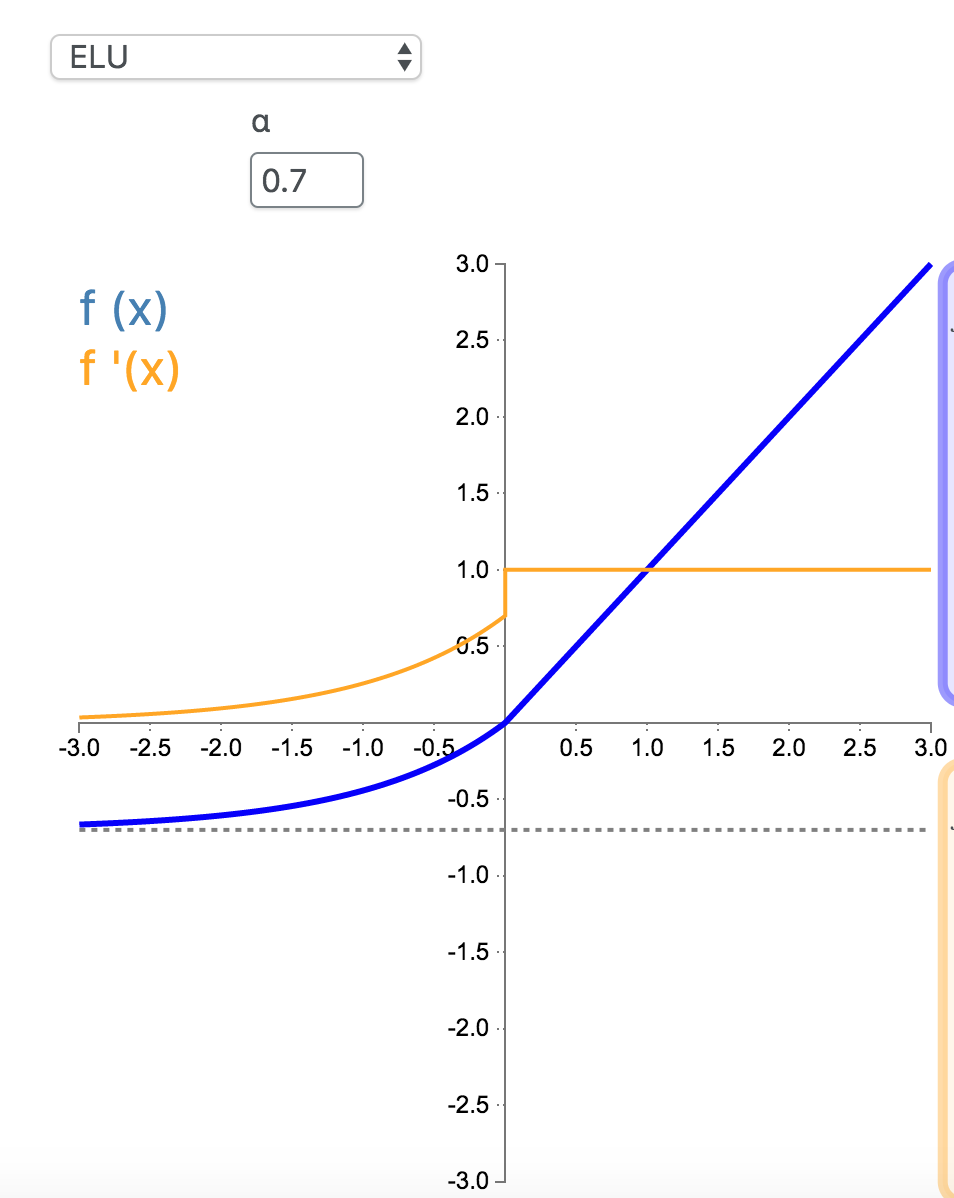
指数线性单元(Exponential Linear Unit,ELU)也属于 ReLU 修正类激活函数的一员。和 PReLU 以及 RReLU 类似,为负值输入添加了一个非零输出。和其它修正类激活函数不同的是,它包括一个负指数项,从而防止静默神经元出现,导数收敛为零,从而提高学习效率。
\[
f(x) = \begin{cases}\alpha(e^x - 1) & \text{for } x < 0\\x & \text{for } x \ge 0\end{cases}
\]
\[
f'(x) = \begin{cases} \alpha e^{x} = f(x) + \alpha & \text{for } x < 0\\1 & \text{for } x \ge 0\end{cases}
\]
\(\alpha = 0.7\):
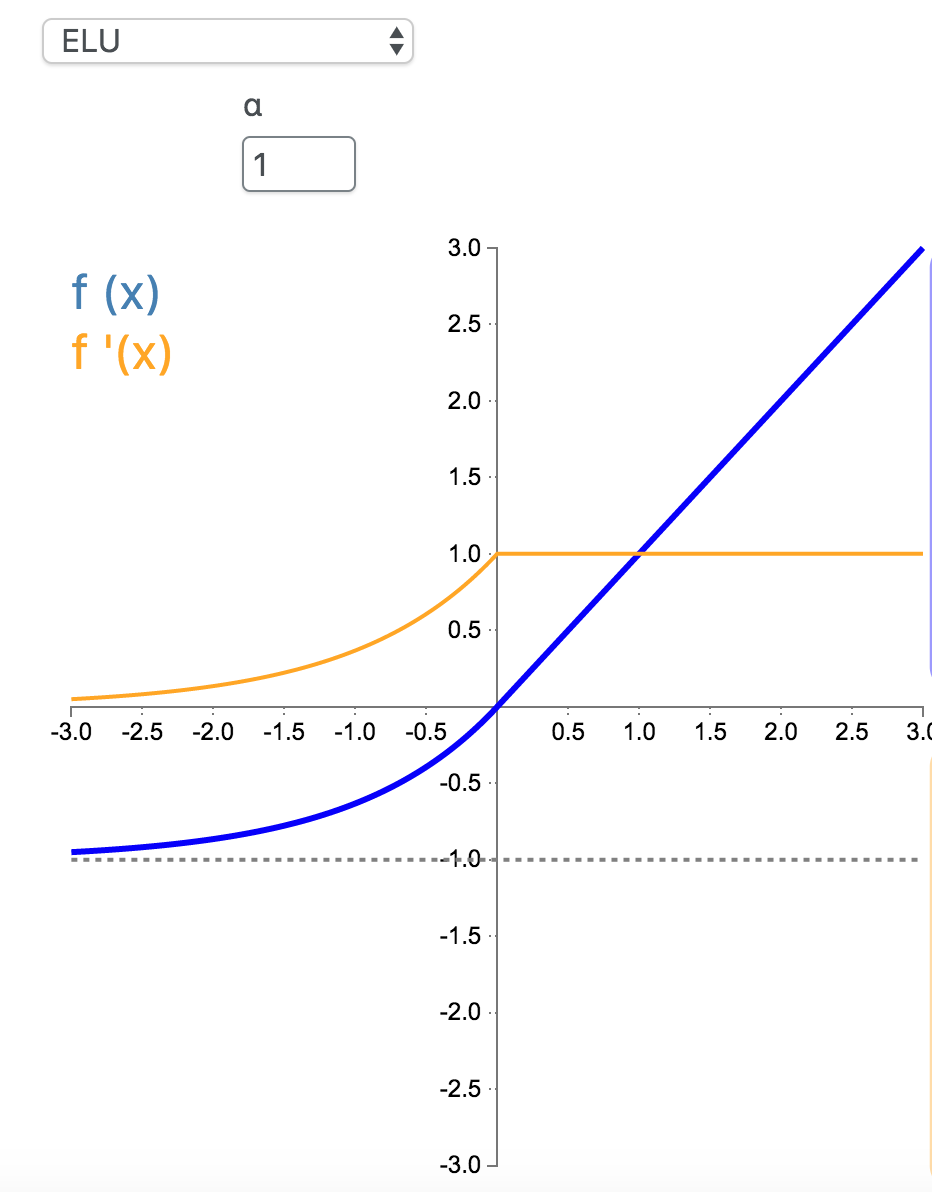
\(\alpha = 1\):
注:
tensorflow中的实现就是\(\alpha = 1\)的版本tensorflow/tensorflow/core/kernels/relu_op_functor.h:
// Functor used by EluOp to do the computations.
template <typename Device, typename T>
struct Elu {
// Computes Elu activation.
//
// features: any shape.
// activations: same shape as "features".
void operator()(const Device& d, typename TTypes<T>::ConstTensor features,
typename TTypes<T>::Tensor activations) {
// features.constant(?)
activations.device(d) =
(features < static_cast<T>(0))
.select(features.exp() - features.constant(static_cast<T>(1)),
features);
}
};
// Functor used by EluGradOp to do the computations.
template <typename Device, typename T>
struct EluGrad {
// Computes EluGrad backprops.
//
// gradients: gradients backpropagated to the Elu op.
// activations: outputs of the Elu op.
// backprops: gradients to backpropagate to the Elu inputs.
void operator()(const Device& d, typename TTypes<T>::ConstTensor gradients,
typename TTypes<T>::ConstTensor activations,
typename TTypes<T>::Tensor backprops) {
backprops.device(d) =
(activations < static_cast<T>(0))
.select((activations + static_cast<T>(1)) * gradients, gradients);
}
};
10. SELU
参考
引爆机器学习圈:「自归一化神经网络」提出新型激活函数SELU
如何评价 Self-Normalizing Neural Networks 这篇论文?
paper: Self-Normalizing Neural Networks
其实就是ELU乘了个lambda,关键在于这个lambda是大于1的。以前relu,prelu,elu这些激活函数,都是在负半轴坡度平缓,这样在activation的方差过大的时候可以让它减小,防止了梯度爆炸,但是正半轴坡度简单的设成了1。而selu的正半轴大于1,在方差过小的的时候可以让它增大,同时防止了梯度消失。这样激活函数就有一个不动点,网络深了以后每一层的输出都是均值为0方差为1。
\[
f(x) = \lambda \begin{cases}\alpha(e^x - 1) & \text{for } x < 0\\x & \text{for } x \ge 0 \end{cases}\\\text{ with } \lambda = 1.0507, \alpha = 1.67326
\]
\[
f'(x) = \begin{cases}\lambda\alpha e^{x} = (f(x) + \lambda \alpha) & \text{for } x < 0\\\lambda & \text{for } x \ge 0\end{cases}
\]
tensorflow中的实现tensorflow/tensorflow/core/kernels/relu_op_functor.h:
// Functor used by SeluOp to do the computations.
template <typename Device, typename T>
struct Selu {
// Computes Selu activation.
//
// features: any shape.
// activations: same shape as "features".
void operator()(const Device& d, typename TTypes<T>::ConstTensor features,
typename TTypes<T>::Tensor activations) {
// features.constant(?)
const auto scale = static_cast<T>(1.0507009873554804934193349852946);
const auto scale_alpha = static_cast<T>(1.7580993408473768599402175208123);
const auto one = static_cast<T>(1);
const auto zero = static_cast<T>(0);
activations.device(d) =
(features < zero)
.select(scale_alpha * (features.exp() - features.constant(one)),
scale * features);
}
};
// Functor used by SeluGradOp to do the computations.
template <typename Device, typename T>
struct SeluGrad {
// Computes SeluGrad backprops.
//
// gradients: gradients backpropagated to the Selu op.
// activations: outputs of the Selu op.
// backprops: gradients to backpropagate to the Selu inputs.
void operator()(const Device& d, typename TTypes<T>::ConstTensor gradients,
typename TTypes<T>::ConstTensor activations,
typename TTypes<T>::Tensor backprops) {
const auto scale = static_cast<T>(1.0507009873554804934193349852946);
const auto scale_alpha = static_cast<T>(1.7580993408473768599402175208123);
backprops.device(d) =
(activations < static_cast<T>(0)).select(
gradients * (activations + scale_alpha), gradients * scale);
}
};
11. SReLU
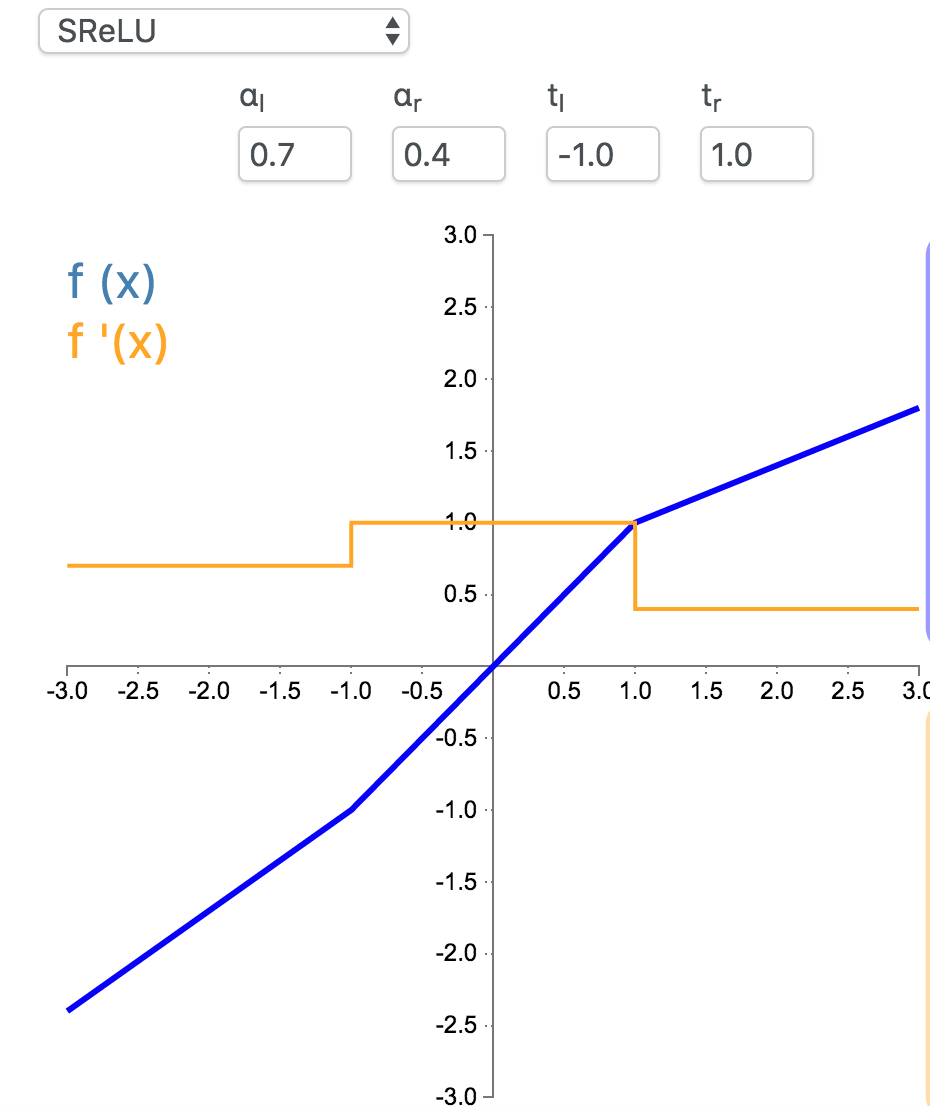
S 型整流线性激活单元(S-shaped Rectified Linear Activation Unit,SReLU)属于以 ReLU 为代表的整流激活函数族。它由三个分段线性函数组成。其中两种函数的斜度,以及函数相交的位置会在模型训练中被学习。
\[
f_{t_l,a_l,t_r,a_r}(x) = \begin{cases}t_l + a_l (x - t_l) & \text{for } x \le t_l\\x & \text{for } t_l < x < t_r\\t_r + a_r (x - t_r) & \text{for } x \ge t_r\end{cases}
\]
\[
f'_{t_l,a_l,t_r,a_r}(x) = \begin{cases}a_l & \text{for } x \le t_l\\1 & \text{for } t_l < x < t_r\\a_r & \text{for } x \ge t_r\end{cases}
\]
12. Hard Sigmoid
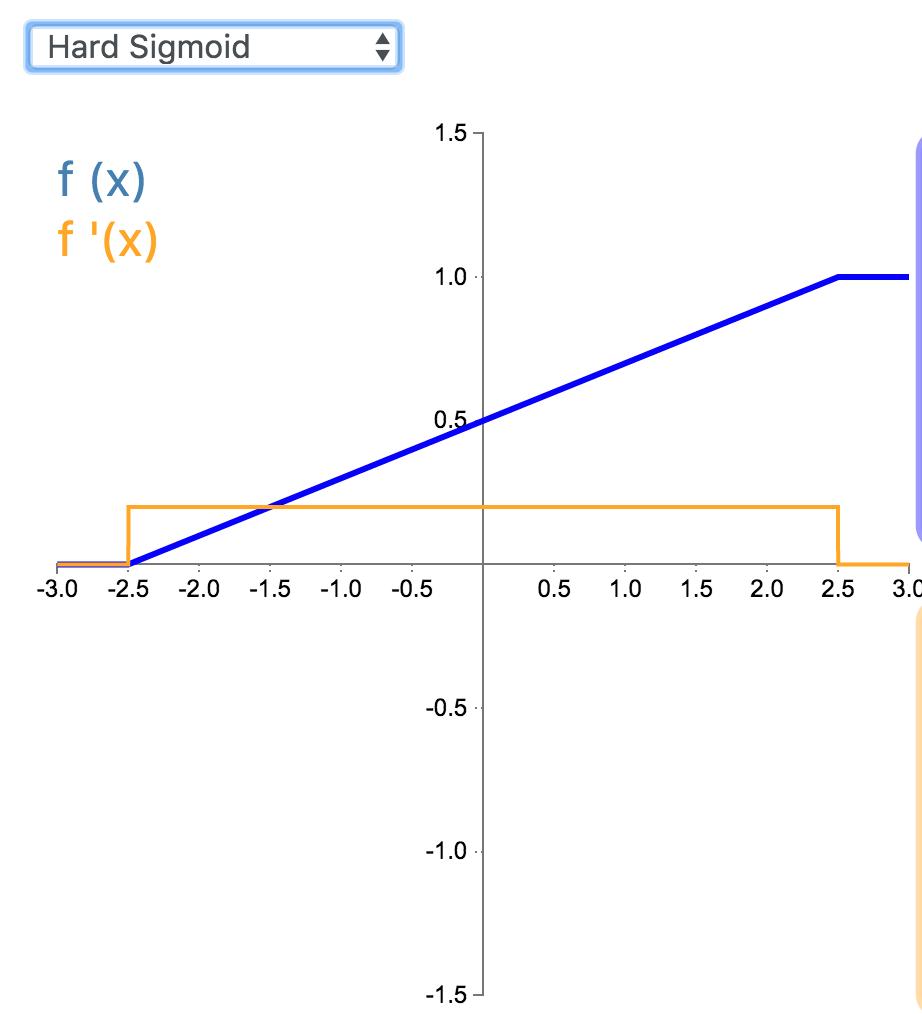
Hard Sigmoid 是 Logistic Sigmoid 激活函数的分段线性近似。它更易计算,这使得学习计算的速度更快,尽管首次派生值为零可能导致静默神经元/过慢的学习速率(详见 ReLU)。
\[
f(x) =\begin{cases}0 & \text{for } x<-2.5\\0.2x + 0.5 & \text{for } -2.5\geq x\leq 2.5 \\1 & \text{for } x>2.5\end{cases}
\]
\[
f(x) =\begin{cases}0 & \text{for } x<-2.5\\0.2 & \text{for } -2.5\geq x\leq 2.5 \\0 & \text{for } x>2.5\end{cases}
\]
13. Hard Tanh
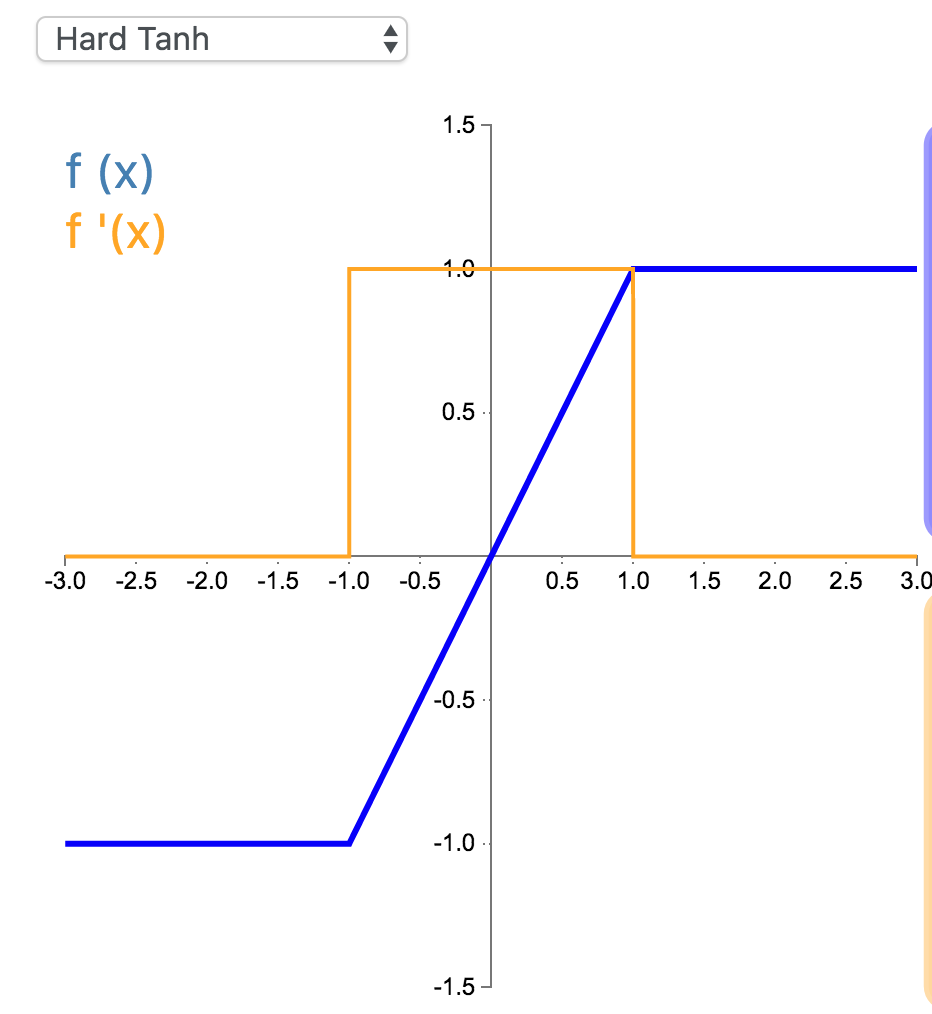
Hard Tanh 是 Tanh 激活函数的线性分段近似。相较而言,它更易计算,这使得学习计算的速度更快,尽管首次派生值为零可能导致静默神经元/过慢的学习速率(详见 ReLU)。
\[
f(x) =\begin{cases}-1 & \text{for } x<-1\\x & \text{for } -1\geq x\leq 1 \\1 & \text{for } x>1\end{cases}
\]
\[
f(x) =\begin{cases}0 & \text{for } x<-1\\1 & \text{for } -1\geq x\leq 1 \\0 & \text{for } x>1\end{cases}
\]
14. LeCun Tanh
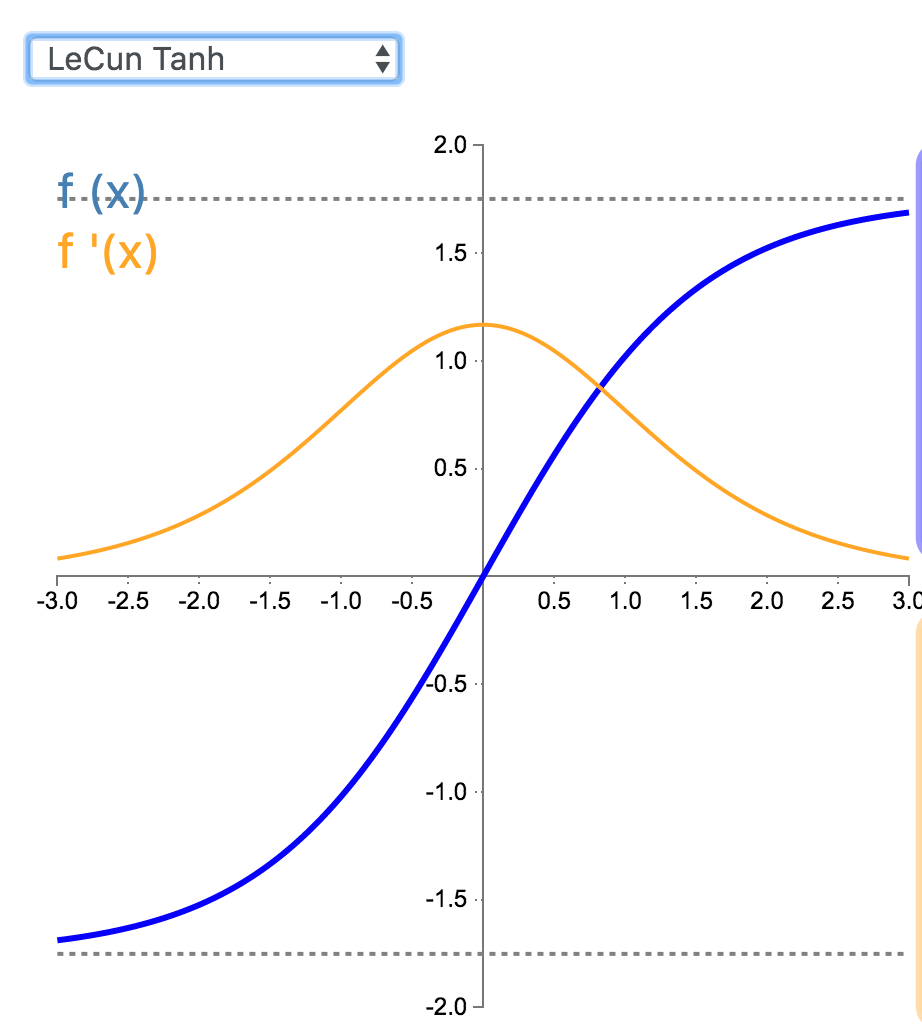
LeCun Tanh(也被称作 Scaled Tanh)是 Tanh 激活函数的扩展版本。它具有以下几个可以改善学习的属性:f(± 1) = ±1;二阶导数在 x=1 最大化;且有效增益接近 1。
\[
\begin{align*}f(x)&=1.7519\tanh(\frac{2}{3}x)\end{align*}
\]
\[
\begin{align*}f'(x)&=1.7519*\frac{2}{3}(1-\tanh^2(\frac{2}{3}x))\\&=1.7519*\frac{2}{3}-\frac{2}{3*1.7519}f(x)^2\end{align*}
\]
15. ArcTan
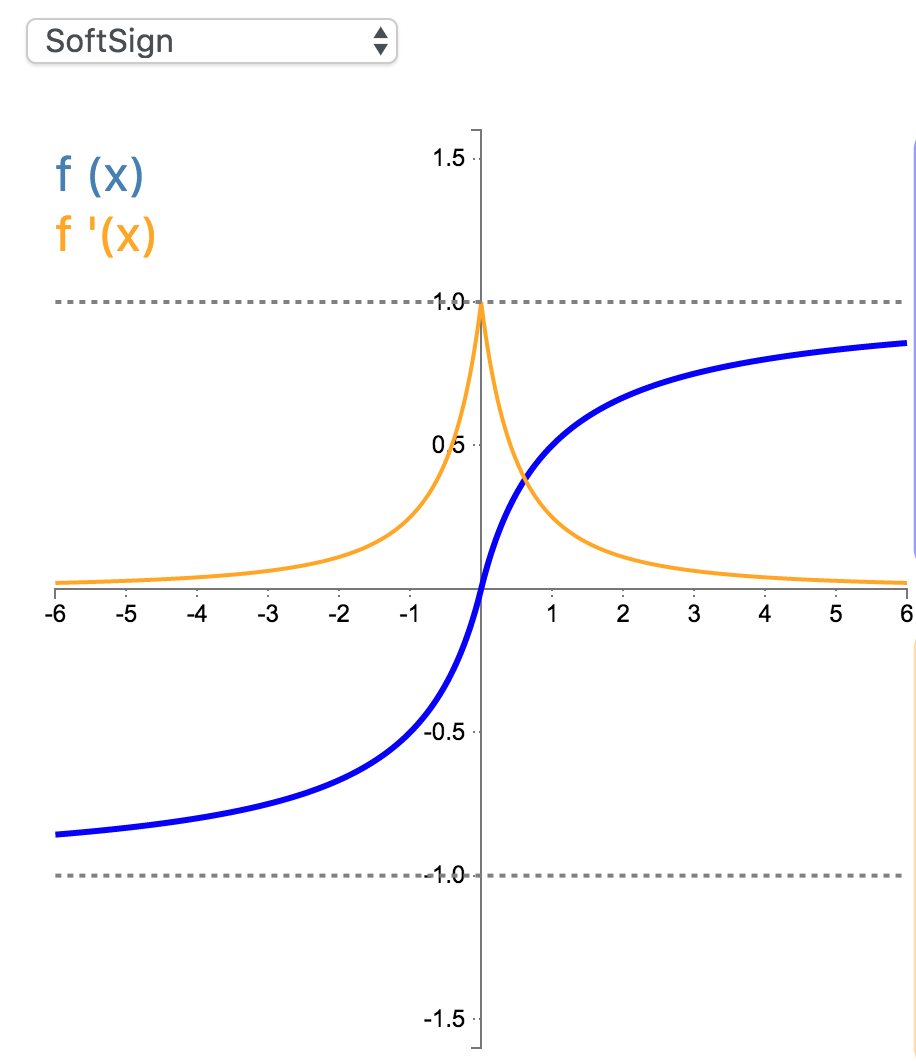
16. SoftSign
Softsign 是 Tanh 激活函数的另一个替代选择。就像 Tanh 一样,Softsign 是反对称、去中心、可微分,并返回-1 和 1 之间的值。其更平坦的曲线与更慢的下降导数表明它可以更高效地学习。
\[
f(x)=\frac{x}{1+|x|}, f(x) \in (-1,1)
\]
\[
f'(x)=\frac{1}{(1+|x|)^2}, f'(x) \in (0,1]
\]
tensorflow实现tensorflow/tensorflow/core/kernels/softsign_op.h:
// Functor used by SoftsignOp to do the computations.
template <typename Device, typename T>
struct Softsign {
// Computes Softsign activation.
//
// features: any shape.
// activations: same shape as "features".
void operator()(const Device& d, typename TTypes<T>::ConstTensor features,
typename TTypes<T>::Tensor activations) {
activations.device(d) =
features / (features.abs() + features.constant(T(1)));
}
};
// Functor used by SoftsignGradOp to do the computations.
template <typename Device, typename T>
struct SoftsignGrad {
// Computes SoftsignGrad backprops.
//
// gradients: gradients backpropagated to the Softsign op.
// features: inputs that were passed to the Softsign op.
// backprops: gradients to backpropagate to the Softsign inputs.
void operator()(const Device& d, typename TTypes<T>::ConstTensor gradients,
typename TTypes<T>::ConstTensor features,
typename TTypes<T>::Tensor backprops) {
backprops.device(d) =
gradients / (features.abs() + features.constant(T(1))).square();
}
};
17. SoftPlus
18. Signum
19. Bent Identity
20. Symmetrical Sigmoid
21. Log Log
22. Gaussian
23. Absolute
24. Sinusoid
25. Cos
注意区分:两个向量的cos相似度(例如作为loss_layer)的求导: https://math.stackexchange.com/questions/1923613/partial-derivative-of-cosine-similarity