深入浅出强化学习-chap13 值迭代网络
标签:值迭代网络, value iteration network目录
参考《深入浅出强化学习》
1. 背景
参考 https://zhuanlan.zhihu.com/p/25515755
slide:https://daiwk.github.io/assets/value-iteration-networks-slide.pdf
1.1 DQN的缺陷
先从以下几个角度来理解DQN:
- DQN是一个深度神经网络:是一个由3个卷积层和2个全连接层组成的深度神经网络
- DQN的训练方法是强化学习:调整神经网络权值有很多方法,只是在DQN中使用的是强化学习。详见第6章(https://daiwk.github.io/posts/rl-stepbystep-chap6.html)
Tamar等发现,已经调优的深度神经网络,很难泛化到其他游戏中,即,该网络并没有学到本质。。。
原因就在于,DQN的网络结构是前向的多层神经网络。输入是状态,输出是动作,也就是策略。Tamar等人称这种策略为『reactive policy(反应式策略)』。也就是给定一个状态,得到一个反应动作。
从强化学习要解决的任务来看,强化学习要解决的是序贯决策问题,即当前的决策要考虑后续的决策,使得整个策略总体最优,而反应式策略并不能表达后续策略对当前策略的影响。。
2.2 具有规划能力的策略网络
所谓的规划就是考虑后续的回报。目前大部分强化学习所用的深度网络都是反应是网络,缺少显式的规划计算。但由于训练方法用的是强化学习训练方法,在训练时考虑了规划问题,所以很多网络还是比较成功的。但由于网络本身没有规划模块,所以运用到新环境时,大部分需要重新训练,即泛化能力差。
如果训练策略本身有规划模块,有以下两个好处:
- 可以利用已经训练好的规划模块规划新的任务,泛化能力很强
- 训练方法可以更灵活,不必依赖强化学习算法。可以利用成熟的监督学习方法和模仿学习方法。而,如果没有数据标签时,仍然要用强化学习的训练方法。
2. 值迭代网络
最常用的规划算法是值迭代算法,第3章讲了动态规划的思想。规划实际蕴含的是一个优化问题,基于贝尔曼优化原理:
\[
\upsilon ^*(s)=\underset{a}{max}R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon ^*(s')
\]
基于该原理,具体的算法实现是值迭代算法,在第3章中提到了https://daiwk.github.io/posts/rl-stepbystep-chap3.html#13-%E5%80%BC%E5%87%BD%E6%95%B0%E8%BF%AD%E4%BB%A3%E7%AE%97%E6%B3%95:
- 输入:状态转移概率
\(P^a_{ss'}\),回报函数\(R^a_{s}\),折扣因子\(\gamma\),初始化值函数\(\upsilon(s)=0\),初始化策略\(\pi_0\)- Repeat
\(l=0,1,...\)- for every
\(s\)do\(\upsilon _{l+1}(s)=\underset{a}{max}R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon _l(s')\)- Until
\(\upsilon _{l+1}=\upsilon _l\)- 输出:
\(\pi(s)=argmax_aR^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon _l(s')\)
由于值迭代的计算过程与CNN的传播过程很相似,所以可以利用CNN来表示值迭代过程。
先看看值迭代计算过程与CNN传播过程的相似之处:
值迭代中,最关键的公式是:
\[
\upsilon _{l+1}(s)=\underset{a}{max}R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon _l(s')
\]
可以分解为两个步骤:
- 遍历动作
\(a\),得到不同动作\(a\)对应的值函数更新,即:
\[
\upsilon _{l+1}(s)=R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon _l(s')
\]
这一步相当于CNN中的卷积操作。相当于图中的,输入\(\bar{R}\)和\(Prev.\ Value\),得到\(\bar{Q}\)
- 遍历动作
\(a\),找到最大的\(\upsilon_{l+1}(s,a)\):
\[
\upsilon _{l+1}(s)=\underset{a}{max}\upsilon _{l+1}(s,a)
\]
这一步相当于CNN中的池化操作。相当于图中的,输入\(\bar{Q}\),得到\(New\ Value\ \bar{V}\)
所以,可以将值迭代的过程用CNN嵌入到策略网络中,而与CNN有如下的不同:
- 偏移量
\(R^a_s\)对应着每个像素的偏移量(bias) - 状态转移函数
\(P^a_{ss'}\)对应着卷积核,因为它要和\(\bar{V}\)进行点积再求和 - 卷积核的个数对应着动作空间的维数
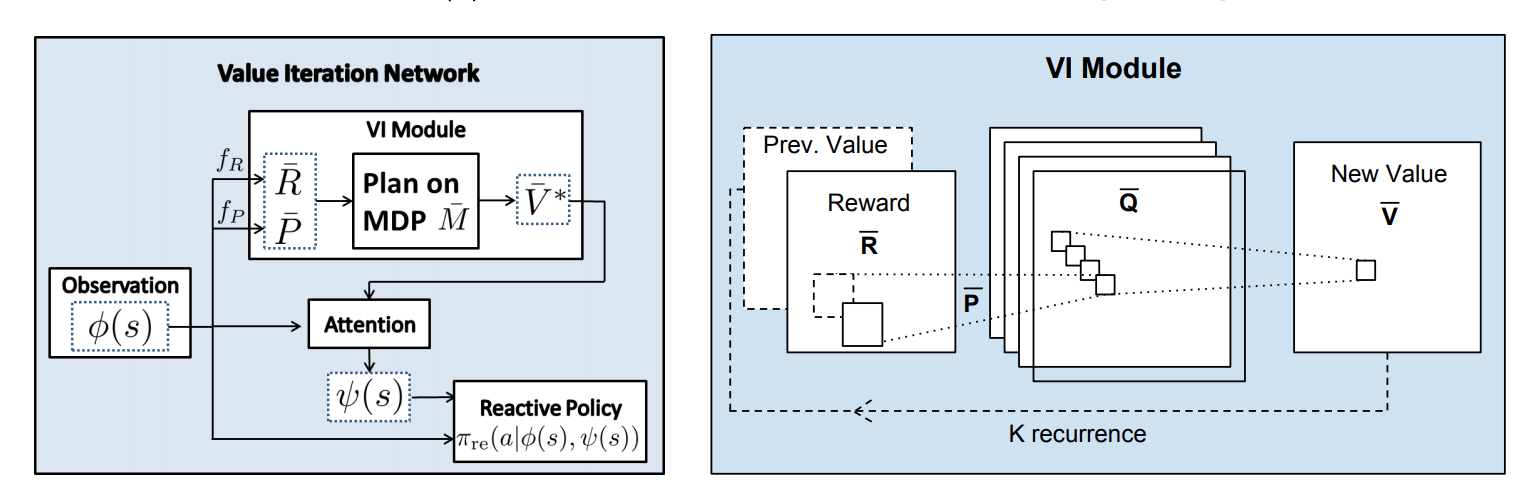
这个网络迭代k次,可以理解为网络往后多看了k步之后的值函数。【相当于一个k个时间步的cnn(conv+maxpooling),然后再和原始输入做个attention?】
k步之后得到的最优策略为:
\[
\pi ^*(s)=argmax_aR(s,a)+\gamma \sum _{s'} P(s'|s,a)V^*(s')
\]
状态\(s\)处的策略只和它的邻域的值函数\(V^*(s')\)有关。而在nn中,当给定的标签只与输入特征的一个局部相关时,就是attention机制。所以,VIN在VI模块后,加了一个attention网络。
训练方法的话,可以采用模仿学习(IL),也可以采用强化学习(RL)。模仿学习就是利用专家数据对网络参数进行训练,例如针对导航任务,专家数据可以来自传统的规划算法,如Dijkstra算法或者\(A^*\)算法。
3. 代码解读
tf:https://github.com/TheAbhiKumar/tensorflow-value-iteration-networks
pytorch:https://github.com/kentsommer/pytorch-value-iteration-networks
tf版本
3.1 基础知识:
python的slice函数
class slice(stop)
class slice(start, stop[, step])
### start -- 起始位置
### stop -- 结束位置
### step -- 间距
## 示例
>>>myslice = slice(5) # 设置截取5个元素的切片
>>> myslice
slice(None, 5, None)
>>> arr = range(10)
>>> arr
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> arr[myslice] # 截取 5 个元素
[0, 1, 2, 3, 4]
>>>
tf.nn.conv2d
参考https://daiwk.github.io/posts/knowledge-tf-usage.html#tfnnconv2d
tf.reduce_*
参考https://daiwk.github.io/posts/knowledge-tf-usage.html#tfreduce_
3.2 代码
def flipkernel(kern):
return kern[(slice(None, None, -1),) * 2 + (slice(None), slice(None))]
def conv2d_flipkernel(x, k, name=None):
return tf.nn.conv2d(x, flipkernel(k), name=name,
strides=(1, 1, 1, 1), padding='SAME')
def VI_Block(X, S1, S2, config):
k = config.k # Number of value iterations performed
ch_i = config.ch_i # Channels in input layer
ch_h = config.ch_h # Channels in initial hidden layer
ch_q = config.ch_q # Channels in q layer (~actions)
state_batch_size = config.statebatchsize # k+1 state inputs for each channel
bias = tf.Variable(np.random.randn(1, 1, 1, ch_h) * 0.01, dtype=tf.float32)
# weights from inputs to q layer (~reward in Bellman equation)
w0 = tf.Variable(np.random.randn(3, 3, ch_i, ch_h) * 0.01, dtype=tf.float32) # 从X到h?
w1 = tf.Variable(np.random.randn(1, 1, ch_h, 1) * 0.01, dtype=tf.float32) # 从h到reward?
w = tf.Variable(np.random.randn(3, 3, 1, ch_q) * 0.01, dtype=tf.float32) # 从reward到q?
# feedback weights from v layer into q layer (~transition probabilities in Bellman equation)
w_fb = tf.Variable(np.random.randn(3, 3, 1, ch_q) * 0.01, dtype=tf.float32)
w_o = tf.Variable(np.random.randn(ch_q, 8) * 0.01, dtype=tf.float32)
# initial conv layer over image+reward prior
h = conv2d_flipkernel(X, w0, name="h0") + bias
r = conv2d_flipkernel(h, w1, name="r")
q = conv2d_flipkernel(r, w, name="q")
v = tf.reduce_max(q, axis=3, keep_dims=True, name="v") # 相当于maxpooling
for i in range(0, k-1):
rv = tf.concat([r, v], 3) # reward和上一步的v一起,接下来进行卷积
wwfb = tf.concat([w, w_fb], 2)
q = conv2d_flipkernel(rv, wwfb, name="q")
v = tf.reduce_max(q, axis=3, keep_dims=True, name="v")
# do one last convolution
q = conv2d_flipkernel(tf.concat([r, v], 3),
tf.concat([w, w_fb], 2), name="q")
# CHANGE TO THEANO ORDERING
# Since we are selecting over channels, it becomes easier to work with
# the tensor when it is in NCHW format vs NHWC
q = tf.transpose(q, perm=[0, 3, 1, 2])
# Select the conv-net channels at the state position (S1,S2).
# This intuitively corresponds to each channel representing an action, and the convnet the Q function.
# The tricky thing is we want to select the same (S1,S2) position *for each* channel and for each sample
# TODO: performance can be improved here by substituting expensive
# transpose calls with better indexing for gather_nd
bs = tf.shape(q)[0]
rprn = tf.reshape(tf.tile(tf.reshape(tf.range(bs), [-1, 1]), [1, state_batch_size]), [-1])
ins1 = tf.cast(tf.reshape(S1, [-1]), tf.int32)
ins2 = tf.cast(tf.reshape(S2, [-1]), tf.int32)
idx_in = tf.transpose(tf.stack([ins1, ins2, rprn]), [1, 0])
q_out = tf.gather_nd(tf.transpose(q, [2, 3, 0, 1]), idx_in, name="q_out")
# add logits
logits = tf.matmul(q_out, w_o)
# softmax output weights
output = tf.nn.softmax(logits, name="output")
return logits, output