传统ctr预估
标签:ctr预估, lr+gbdt目录
1. 传统方法:
1.1 LR+GBDT
1.1.1 LR
LR映射后的函数值就是CTR的预估值。这种线性模型很容易并行化,处理上亿条训练样本不是问题,但线性模型学习能力有限,需要大量特征工程预先分析出有效的特征、特征组合,从而去间接增强LR 的非线性学习能力。
LR模型中的特征组合很关键,但又无法直接通过特征笛卡尔积 解决,只能依靠人工经验,耗时耗力同时并不一定会带来效果提升。
1.1.2 GBDT
参考http://www.jianshu.com/p/005a4e6ac775
GBDT又叫MART(Multiple Additive Regression Tree),GBDT中的树是回归树(不是分类树),GBDT用来做回归预测,调整后也可以用于分类。每次迭代都在减少残差的梯度方向新建立一颗决策树,迭代多少次就会生成多少颗决策树。GBDT的思想使其具有天然优势,可以发现多种有区分性的特征以及特征组合,决策树的路径可以直接作为LR输入特征使用,省去了人工寻找特征、特征组合的步骤。这种通过GBDT生成LR特征的方式(GBDT+LR),业界已有实践(Facebook,Kaggle-2014),且效果不错。
1.1.2.1 回归树
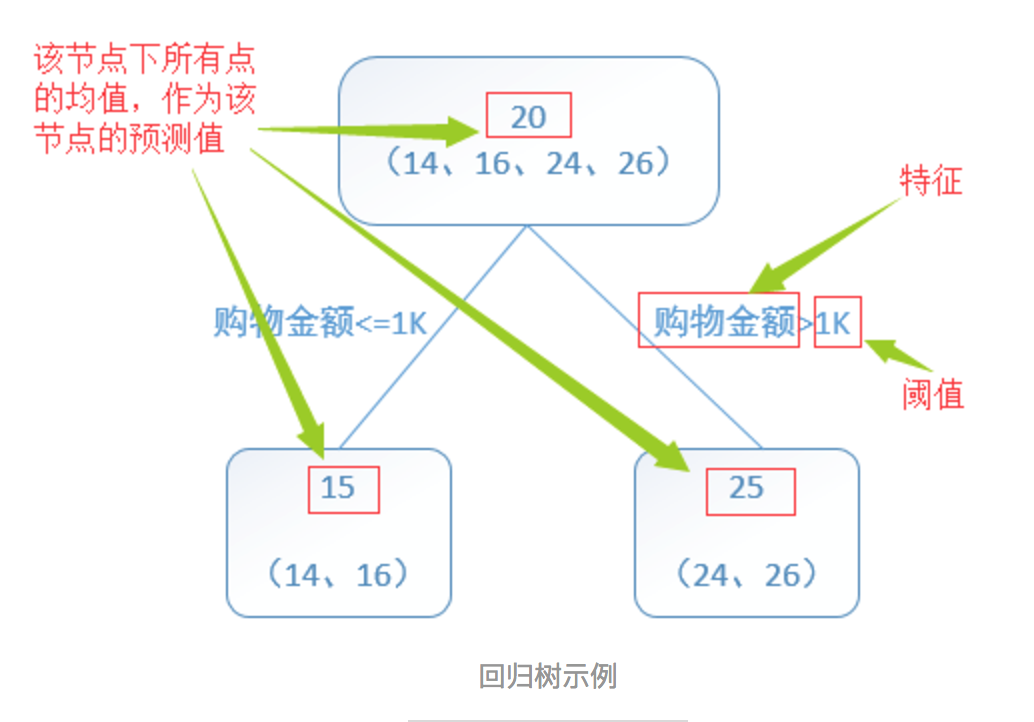
回归树总体流程类似于分类树,区别在于,回归树的每一个节点都会得一个预测值,以年龄为例,该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点,但衡量最好的标准不再是最大熵,而是最小化平方误差。也就是被预测出错的人数越多,错的越离谱,平方误差就越大,通过最小化平方误差能够找到最可靠的分枝依据。分枝直到每个叶子节点上人的年龄都唯一或者达到预设的终止条件(如叶子个数上限),若最终叶子节点上人的年龄不唯一,则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。
参考http://blog.csdn.net/puqutogether/article/details/44593647
算法如下:

参考http://blog.csdn.net/suranxu007/article/details/49910323
1.1.2.2 提升树算法(Boosting Decision Tree)
提升树是迭代多棵回归树来共同决策。当采用平方误差损失函数时,每一棵回归树学习的是之前所有树的结论和残差,拟合得到一个当前的残差回归树,残差的意义如公式:残差 = 真实值 - 预测值 。提升树即是整个迭代过程生成的回归树的累加。
训练集是4个人,A,B,C,D年龄分别是14,16,24,26。样本中有购物金额、上网时长、经常到百度知道提问等特征。 参考http://blog.csdn.net/suranxu007/article/details/49910323
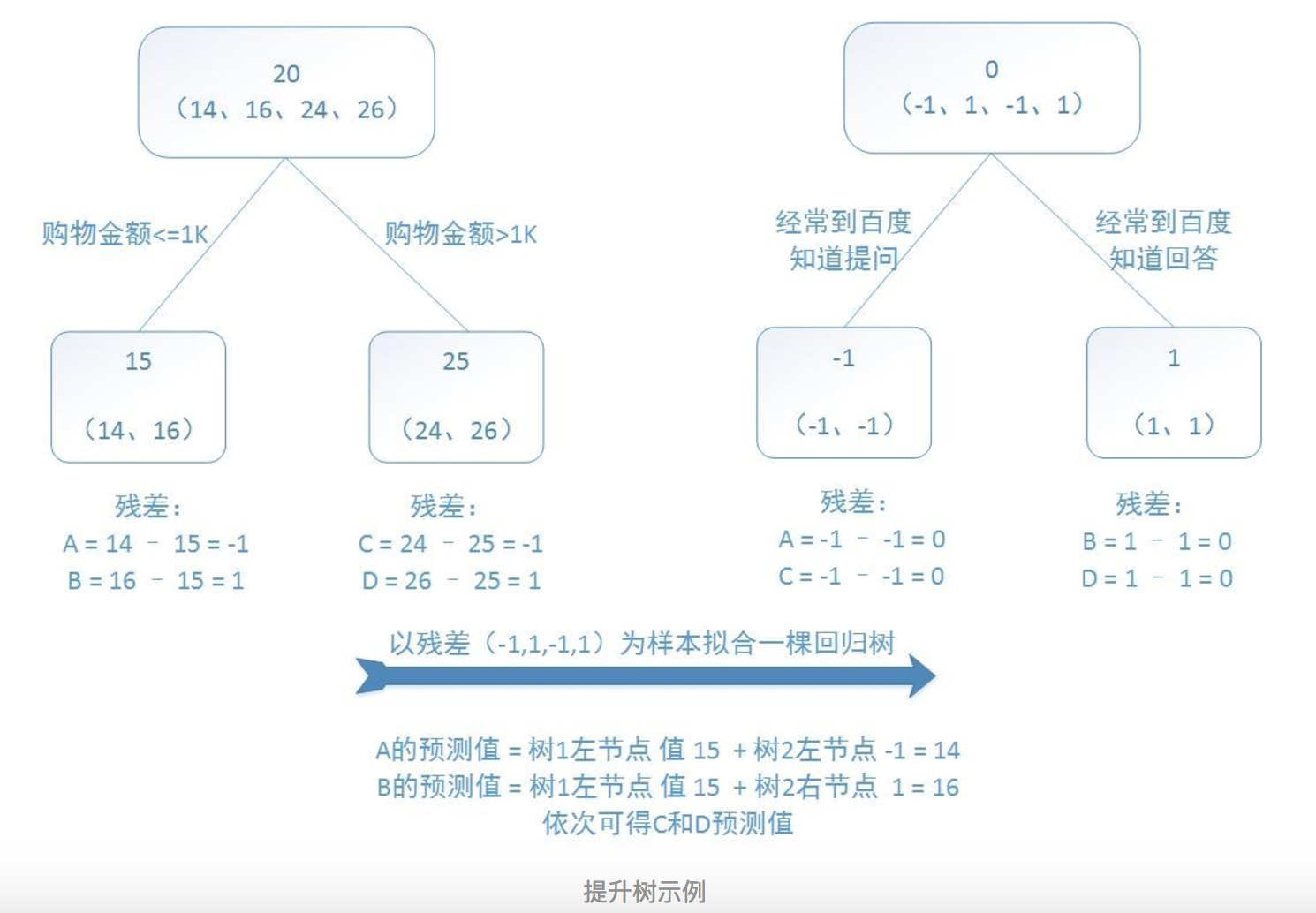
预测值等于所有树值得累加,如A的预测值 = 树1左节点 值 15 + 树2左节点 -1 = 14。 算法如下:

1.1.2.3 GBDT
提升树利用加法模型和前向分步算法实现学习的优化过程。当损失函数是平方损失和指数损失函数时,每一步的优化很简单,如平方损失函数学习残差回归树。常见损失函数及其梯度如下:

但对于一般的损失函数,往往每一步优化没那么容易,如上图中的绝对值损失函数和Huber损失函数。针对这一问题,Freidman提出了梯度提升算法:利用最速下降的近似方法,即利用损失函数的负梯度在当前模型的值,作为回归问题中提升树算法的残差的近似值,拟合一个回归树。(注:鄙人私以为,与其说负梯度作为残差的近似值,不如说残差是负梯度的一种特例)算法如下

算法步骤解释:
1、初始化,估计使损失函数极小化的常数值,它是只有一个根节点的树,即ganma是一个常数值。 2、 (a)计算损失函数的负梯度在当前模型的值,将它作为残差的估计 (b)估计回归树叶节点区域,以拟合残差的近似值 (c)利用线性搜索估计叶节点区域的值,使损失函数极小化 (d)更新回归树 3、得到输出的最终模型 f(x)
1.1.2.4 参数设置
推荐GBDT树的深度:6;(横向比较:DecisionTree/RandomForest需要把树的深度调到15或更高)
一句话的解释,来自周志华老师的机器学习教科书( 机器学习-周志华):Boosting主要关注降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成;Bagging主要关注降低方差,因此它在不剪枝的决策树、神经网络等学习器上效用更为明显。
Bagging算法是这样做的:每个分类器都随机从原样本中做有放回的采样,然后分别在这些采样后的样本上训练分类器,然后再把这些分类器组合起来。简单的多数投票一般就可以。其代表算法是随机森林。Boosting的意思是这样,他通过迭代地训练一系列的分类器,每个分类器采用的样本分布都和上一轮的学习结果有关。其代表算法是AdaBoost, GBDT。
其实就机器学习算法来说,其泛化误差可以分解为两部分,偏差(bias)和方差(variance)。这个可由下图的式子导出(这里用到了概率论公式D(X)=E(X^2)-[E(X)]^2)。偏差指的是算法的期望预测与真实预测之间的偏差程度,反应了模型本身的拟合能力;方差度量了同等大小的训练集的变动导致学习性能的变化,刻画了数据扰动所导致的影响。这个有点儿绕,不过你一定知道过拟合。 如下图所示,当模型越复杂时,拟合的程度就越高,模型的训练偏差就越小。但此时如果换一组数据可能模型的变化就会很大,即模型的方差很大。所以模型过于复杂的时候会导致过拟合。 当模型越简单时,即使我们再换一组数据,最后得出的学习器和之前的学习器的差别就不那么大,模型的方差很小。还是因为模型简单,所以偏差会很大。
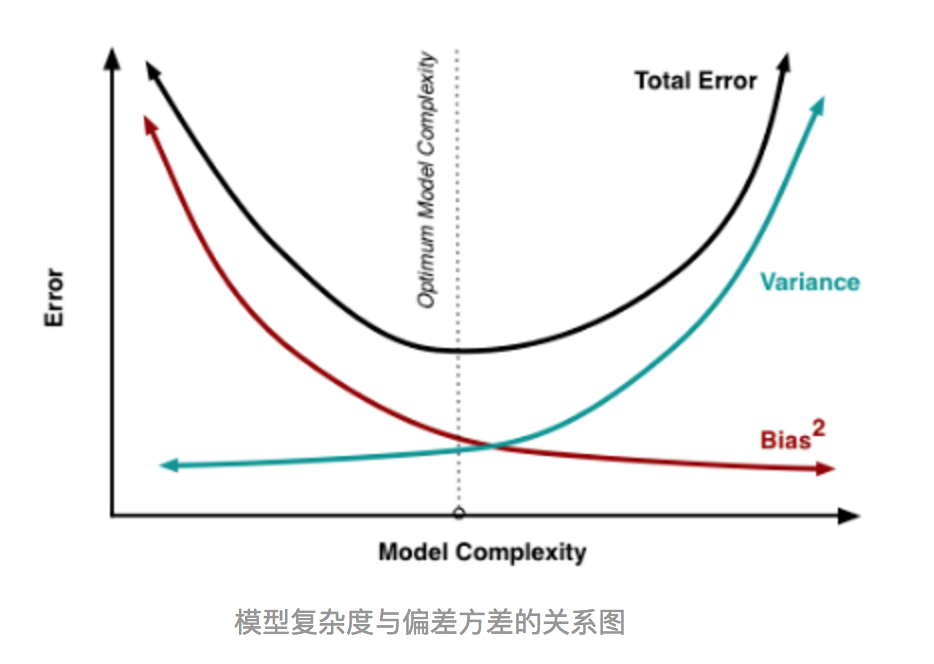
也就是说,当我们训练一个模型时,偏差和方差都得照顾到,漏掉一个都不行。 对于Bagging算法来说,由于我们会并行地训练很多不同的分类器的目的就是降低这个方差(variance) ,因为采用了相互独立的基分类器多了以后,h的值自然就会靠近.所以对于每个基分类器来说,目标就是如何降低这个偏差(bias),所以我们会采用深度很深甚至不剪枝的决策树。 对于Boosting来说,每一步我们都会在上一轮的基础上更加拟合原数据,所以可以保证偏差(bias),所以对于每个基分类器来说,问题就在于如何选择variance更小的分类器,即更简单的分类器,所以我们选择了深度很浅的决策树。
1.1.3 LR+GBDT
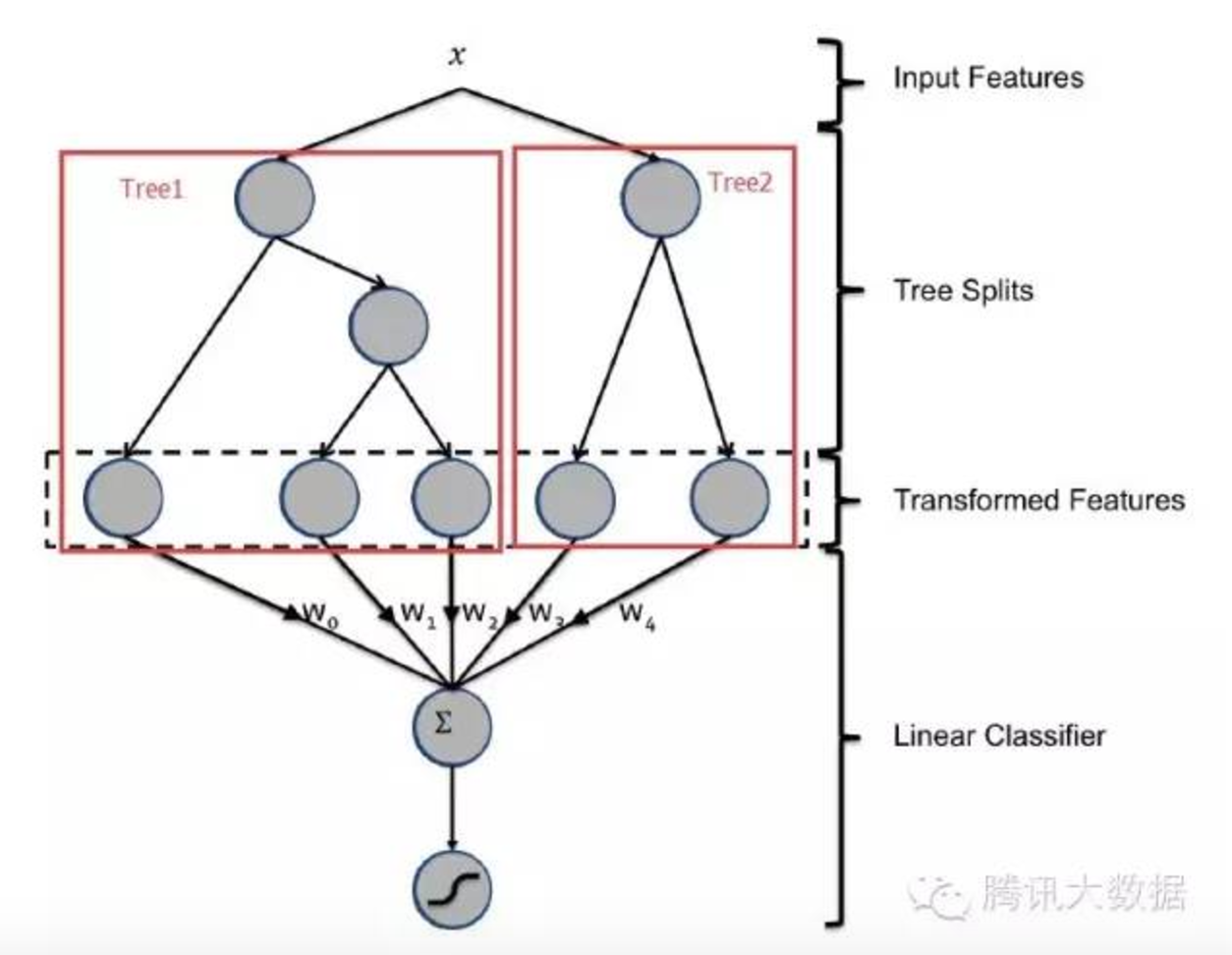
GBDT与LR的融合方式,Facebook的paper有个例子如下图2所示,图中Tree1、Tree2为通过GBDT模型学出来的两颗树,x为一条输入样本,遍历两棵树后,x样本分别落到两颗树的叶子节点上,每个叶子节点对应LR一维特征,那么通过遍历树,就得到了该样本对应的所有LR特征。由于树的每条路径,是通过最小化均方差等方法最终分割出来的有区分性路径,根据该路径得到的特征、特征组合都相对有区分性,效果理论上不会亚于人工经验的处理方式。
另外,RF也是多棵树,但从效果上有实践证明不如GBDT。且GBDT前面的树,特征分裂主要体现对多数样本有区分度的特征;后面的树,主要体现的是经过前N颗树,残差仍然较大的少数样本。优先选用在整体上有区分度的特征,再选用针对少数样本有区分度的特征,思路更加合理,这应该也是用GBDT的原因。
1.1.4 引入id类特征
综合考虑方案如下,使用GBDT建两类树,非ID建一类树,ID建一类树。
1)非ID类树:不以细粒度的ID建树,此类树作为base,即便曝光少的广告、广告主,仍可以通过此类树得到有区分性的特征、特征组合。
2)ID类树:以细粒度 的ID建一类树,用于发现曝光充分的ID对应有区分性的特征、特征组合。如何根据GBDT建的两类树,对原始特征进行映射?以如下图3为例,当一条样本x进来之后,遍历两类树到叶子节点,得到的特征作为LR的输入。当AD曝光不充分不足以训练树时,其它树恰好作为补充。
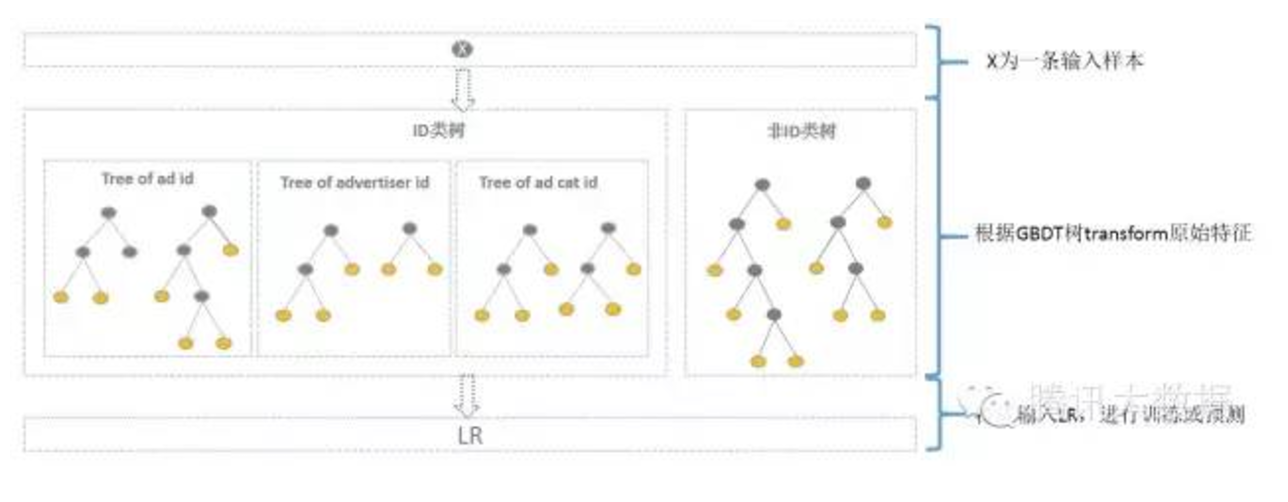
通过GBDT 映射得到的特征空间维度如何?GBDT树有多少个叶子节点,通过GBDT得到的特征空间就有多大。一个叶子节点对应一种有区分性的特征、特征组合,对应LR的一维特征。估算一下,通过GBDT转换得到的特征空间较低,Base树、ID树各N颗,特征空间维度最高为N+N广告数+N广告主数+ N*广告类目数。其中广告数、广告主数、广告类目数都是有限的,同时参考Kaggle竞赛中树的数目N最多为30,则估算通过GBDT 映射得到的特征空间维度并不高,且并不是每个ID训练样本都足以训练多颗树,实际上通过GBDT 映射得到的特征空间维度更低。
如何使用GBDT 映射得到的特征?通过GBDT生成的特征,可直接作为LR的特征使用,省去人工处理分析特征的环节,LR的输入特征完全依赖于通过GBDT得到的特征。此思路已尝试,通过实验发现GBDT+LR在曝光充分的广告上确实有效果,但整体效果需要权衡优化各类树的使用。同时,也可考虑将GBDT生成特征与LR原有特征结合起来使用,待尝试。
2. 基于深度学习的ctr预估模型
基于深度学习的可以参考基于深度学习的ctr预估模型集合(持续更新)